How to add Vectors....

How to Add Vectors

Vectors...

In order to understand how to add vectors, one must first understand, what is a vector? Vectors are comprised of two main characteristics, the magnitude and the direction. Normally, we mainly talk about the magnitude, which is the size of the vector. The size can be speed, distance, acceleration or any other unit. The direction however is not usually discussed about. The direction can be shown as a degree or as a compass direction. A vector can look like this. In order to add two vectors together, you must consider the 2 factors that were mentioned before, the magnitude and the direction. If you have two vectors that are facing the same direction, for example [E] (East), then you can add their magnitudes together and they are both facing the same direction. If they are facing the opposite directions, for example one of them is facing [E] and the other is facing [W], then you may change the one facing [W] to become – [E] since it is the reverse direction of [E]. After that is done, then adding them is a simple matter. A simple example is the picture on the right. The givens are A = 15m [E], B = 30m [W] and C = 10m [W]. Before we add them together, first we must change the direction of A. As you may recall, in order to invert the direction, we merely add the negative sign in front of the magnitude. Therefore A becomes -15m [W]. Now adding them together is very simple. A + B + C = -15 + 30 + 10 = 25m [E].

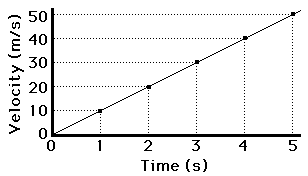
You may wonder, what if they are not complete opposites, what if you had to add a vector facing north with a vector facing east? Well, that is no difficulty whatsoever my young paddlewans. Let’s explain with another example. The graph on the side states that B = 4m [N] while A = 3m [E]. Let’s test your memory; do you remember the Pythagorean Theorem? Well, by using the Pythagorean Theorem, you can find A + B. All you do is find the square root of the sum of “a”, which is A, squared and find the “b”, which is B, squared. You basically get: sqrt(A^2 + B^2) = sqrt(9 + 16) = 25m. WATCH OUT! You may think that you’re done but truth is... IT’S A TRAP! Remember how a vector MUST have both a magnitude and a direction, well, in order to complete A + B, you must find the direction. The direction can be found with trigonometry. First, you label the tail of A (The part of the arrow without the arrow tip) as the origin, then you label the head of B (The part with the arrow tip) as the final point. Now, you use trigonometry to find the angle. Since the tail of A is the origin, think of it on a graph as (0, 0). Therefore, from the graph you realize that A + B is in the positive quadrant.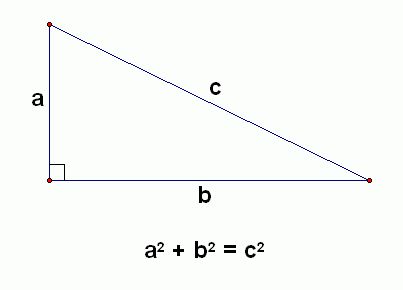 

Pythagorean Theorem

Now find the trigonometry, more specifically tangent. Using tangent, we can find the angle that A + B forms with the y-axis, which becomes 36.7 degrees. With this, we can get A + B = 5 [N36.7E]

Calculating two vectors with diagonals may seem hard but they are actually very simple. Now that you know how to find a diagonal vector from two horizontal/vertical vectors, you just split up the diagonal vectors into a horizontal and a vertical vector, add the 4 different vectors together, find the angle and voila, that becomes your new vector.

How to derive the equation d = v2(delta)t - 1/2a(delta)t^2

Similar to the other equation, d = v1(delta)t + 1/2a(delta)t^2, the equation can be found from a velocity - time graph. First, you have the same graph with the same points. This time, you will find the same area except that you first find the area of a rectangle formed with v2 and (delta)t subtracted by the triangle above the trapezoid. The area of the rectangle is

Area1 = bh

Area1 = (v2)(delta)t

Now, the area of the triangle can be found with the equation Area2 = bh/2. The base of this equation is (delta)t like previously but the height is the difference between v2 and v1, which becomes v2 - v1. Therefore the equation becomes:

Area2 = 1/2(v2 - v1)(delta)t

Now, in order to find the area of the trapezoid, you must subtract the area of the triangle from the rectangle.Therefore, you get

Area = Area1 - Area 2

Area = v2(delta)t - 1/2(v2 - v1)(delta)t

Now label this equation ♦

Previously in class, we learned that acceleration can be derived from the slope of the velocity graph:

a (acceleration) = (v2-v1)/(delta)t

a(delta)t = (v2 - v1)

Now label this ♣

Now substitute ♣ into ♦

d(Area) = v2(delta)t - 1/2 (a(delta)t)(delta)t

d = v2(delta)t - 1/2a(delta)t^2

Thus you derived the equation d = v2(delta)t - 1/2a(delta)t^2.

How to derive the equation d = v1(delta)t + 1/2a(delta)t^2

Velocity Graph with points (v1, t1) and (v2, t2)

First, let's label the first point (v1, t1) where v1 is the velocity at a certain point and t1 is the time at which the velocity v1occurs. Second, let's label the second point (v2, t2) where v2 is another velocity at a certain point and t2 is the time at which v2 occurs. In order to translate the graph into a distance-time graph by finding the total displacement, the area formed with the x-axis must be found. Divide the trapezoid formed into 2 sections, the rectangle and the triangle. The area of the rectangle can be found with the equation Area1 = bh where b is the base, the change in time between t2 and t1 named (delta)t, and where h is the height, v1. Therefore the

Area1 = v1(delta)t

The area of the triangle can be found with the equation Area2 = (bh)/2, where the base is (delta)t and the height is v2 - v1 since you are trying to find the height between v2 and v1. Therefore, your equation is

Velocity Graph with areas indicated of the (tri + rect)angles

Area2 = (v2-v1)(delta)t x 1/2

Area2 = 1/2(v2-v1)(delta)t

Now, let's combine the 2 areas and label it ☺: d(Area) = v1(delta)t + 1/2(v2-v1)(delta)t

Previously in class, we learned that acceleration can be derived from the slope of the velocity graph:

a (acceleration) = (v2-v1)/(delta)t

Now label this ☻                                           a(delta)t = (v2 - v1)

Now substitute ☻ into ☺:                d = v1(delta)t + 1/2(a(delta)t)(delta)t

d = v1(delta)t + 1/2(a (delta)t^2)

d = v1(delta)t + 1/2a(delta)t^2

Thus you derived the equation d = v1(delta)t + 1/2a(delta)t^2.

HARDCORE Velocity and Acceleration hypothesis?

The relation between the velocity and the acceleration is that the area of the shape that the acceleration forms with the-axis is equal to the displacement of the velocity. For example, if acceleration consists of a line going directly from the origin to point (4,4). One could say that the velocity graph, should it be translated would form a parabola with the displacement of 8 with the curve opening upward.  Similarly, the slope of the velocity graph is equal to the acceleration. Should you attempt to find the acceleration from the velocity, you would have to find the instantaneous slope of the parabola and that would give you the acceleration.

Finding the slope of a velocity graph.

The rule however is that if the velocity has a graph with an equation of degree 2, the acceleration must form a graph with an equation of degree1. Similarly, with the velocity is a graph with an equation of degree 5, the acceleration must form a graph with an equation of degree 4. Creating a general rule from this is that if velocity has a graph with an equation of degree n, the acceleration must form a graph with an equation of degree n - 1. This general rule is the basics of derivatives.

Graphs of everything :O

Translating graphs..... to FRENCH!?!?!?!?

Physic Graphs Translated

During the 1^st sec, there was no change in the distance; therefore there is a velocity of zero. From the 1^st to 3^rd sec, there was a constant speed of 1.7m/s east. During the 3^rd – 6^th sec, there was no change in distance; therefore, a velocity of zero. From the 6^th – 7.5 there was a velocity of -2m/s in the opposite direction, west. From then onward, there was no change in distance, therefore velocity as well. Since the velocity was always constant (horizontal line), the acceleration is 0.

From the beginning to the 3^rd second, there was a constant change of position heading west. The constant change was 0.5m/second. From the 3^rd second to the 4^th second, there was no change in distance, therefore a velocity of 0. From the 4^th second to the 5^th second, there was another constant change of position west at the rate of 1m/s. From the 5^th – 7^th second, there was no change in distance so there must be a velocity of 0. From the 7^th second to the end (10^th second) the distance goes to 3m in 3 seconds, which equates to 0.83333 m/s east. Throughout the chart, the velocity was always at a constant rate parallel to the x-axis, therefore the acceleration throughout is 0.

There is a velocity of 0 up to the 2^nd second. From the 2^nd second to the 5^th second, there is a velocity of 0.5m/s. Since there is a constant velocity of 0.5m/s, the distance will increase from 0.5m on the first second, all the way to 1.5m on the 5^th second. From the 5^th second up to the 7^th second, there is a velocity of 0, and the distance does not change. At the 7^th second, there is a sudden velocity of -0.5m/s, which signifies a change of 0.5m/s in the opposite direction. Starting at 1.5m/s the distance will constantly decrease for 3 seconds. 3s x 0.5m/s = 1.5m. The final distance will be 1.5 m. The acceleration is still 0 because of the fact that the velocity stays at a constant rate: in the beginning, the velocity is 0, then the velocity stays at 0.5m/s, then changes back to 0, then finally stays at -0.5ms. Therefore there is no acceleration.

From the 1^st second to the 4^th second, there is a constant change of velocity. The velocity increases by 1/8 or 0.125m/s every second. The distance can be calculated by measuring the velocity of each second and adding them together. At the 4^th second all the way to the 6^th second, there is a constant velocity of 0.4m/s. All you do is add 0.5m/s to the distance every second. At the 6^th second, the velocities reverses from going east to going west at a rate of 0.4m/s for 3 seconds. Since you are moving in the opposite direction, you subtract 0.4m from the distance every second. Finally from the 9^th second to the 10^th second, there is a velocity of 0 and the distance does not change. Since there is a constant change in the velocity, the slope of the change becomes the acceleration. The slope of the constant rise is 2; therefore the acceleration is 2m/s². From there onward, the velocity is either 0 or has a slope of 0 therefore there is no acceleration.

From the start to the 2 and 3/4^th of a second, there is a constant rise in distance. The constant rise becomes the velocity, of 0.1666. From that point to the 6 and 1.2th of a second, there is no change in distance, therefore a velocity of 0. Finally, from the 6 and 1/2th of a second to the end (10^th second) there is a constant rise of distance at a rate of 0.4m/s, which is the velocity. The acceleration is still 0 because the velocity is either on the x-axis or parallel to the x-axis.

During and after the 6th second, the distance is the same as the acceleration

Though this graph may be slightly hard to distinguish, it is relatively easy. From the beginning to the 3^rd second, there is a constant velocity of 0.1666m/s, therefore an increase in the distance. From that point on till the 6 and a half second, there is a constant velocity of -0.1666m/s, which means that there is a decrease in the distance at a rate of 0.1666m every second. Finally, until the end there is a velocity of 0, which means that there is no change in distance. The acceleration may vary according to how you interpret it, but assuming that the slight curve is intentional, there is a slight acceleration of 0.3333m/s and acceleration again of 0.1666m/s. The first acceleration is in the negative region because the velocity is changing from positive to negative, therefore a slope downward. The left hand arrow pose shows that the acceleration must therefore be negative.

By: Kingeon Tsang

The King-Young Motor

The Right-Hand Rule #3, it really sticks out...

On September 30, 2010, we had an in-class assignment to create a motor based on the Right-hand rule #3. The Right-Hand rule #3 applies to an electrically charged rod/wire in between two magnets of opposite poles. It states that when you stretch out your palm, your thumb should go in the direction of which the magnetic fields are travelling. The magnetic fields travel from north to south, so if north is on the right, your thumb points to the left, because the magnetic field moves from the north to south. Your other fingers should point into the direction of which the current is travelling in the rod/wire. If the current travels up, you point your other fingers up, and vice versa. Finally, your palm will then show the direction of which the force will be applied. In the example to the right, the palm is facing towards you-ish to the left-ish that indicates the direction of the electrically charged will move. 

What we hoped for our experiment to turn out to... I guess it's impossible...

Suyoung + Kingeon = UBER PRO H4X0R LEECHERS

With this principle, we had two wires that alternated in rotating, therefore creating a motor. The creation of the motor seemed hard at first since we had to prepare materials, and Suyoung, my partner (leecher), didn’t have that many materials, so he leeched off of me. However, as we put the materials together, it was fairly easy, the nails were straight, the brushes (which we leeched off of Rex) was sanded really well (with sandpaper that we leeched off of Rex), the cork was screwed fairly well (which we leeched off of Mr. Chung) and finally the paperclips (which we leeched off of Mr. Chung) and the thumbtacks (which we leeched off of Lisa + Krystal) worked well. Though I injured myself 2 times, one by the brush/metal thing, and one by a screw, the experiment was fun and our motor was the first smoothest one. Not the first, not the smoothest but the first smoothest =D.