The relation between the velocity and the acceleration is that the area of the shape that the acceleration forms with the-axis is equal to the displacement of the velocity. For example, if acceleration consists of a line going directly from the origin to point (4,4). One could say that the velocity graph, should it be translated would form a parabola with the displacement of 8 with the curve opening upward. Similarly, the slope of the velocity graph is equal to the acceleration. Should you attempt to find the acceleration from the velocity, you would have to find the instantaneous slope of the parabola and that would give you the acceleration.
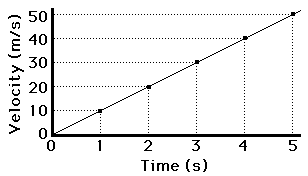 |
| Finding the slope of a velocity graph. |
The rule however is that if the velocity has a graph with an equation of degree 2, the acceleration must form a graph with an equation of degree1. Similarly, with the velocity is a graph with an equation of degree 5, the acceleration must form a graph with an equation of degree 4. Creating a general rule from this is that if velocity has a graph with an equation of degree n, the acceleration must form a graph with an equation of degree n - 1. This general rule is the basics of derivatives.
 |
| Graphs of everything :O |




No comments:
Post a Comment